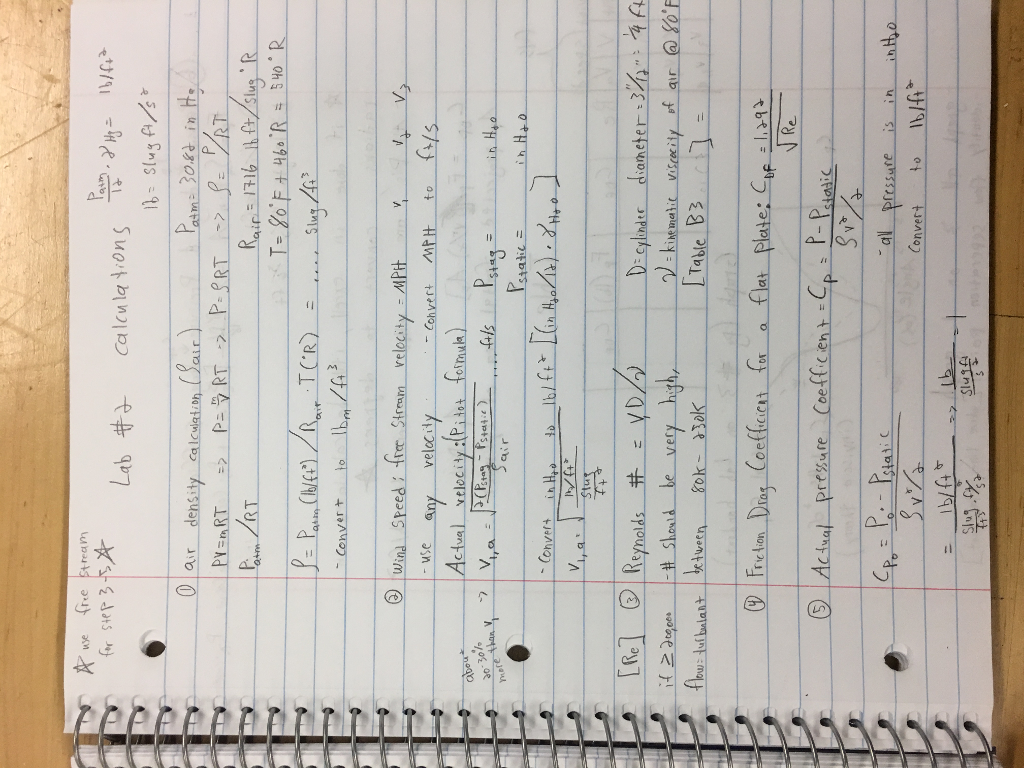The ideal gas equation and the ideal gas constant, which express the ideal gas law provide a means for calculating air density for different pressures and temperatures. Although this article is primarily about determining the density of air, the density of other gases at known temperature and gas pressure can also be estimated using the ideal gas law in the same way. We are all aware that pressure and temperature of the air depend on your location on the earth and the season of the year. And while it is hotter in some seasons than others, pressure and temperature change day to day, hour to hour, sometimes even minute to minute .
The values presented on the slide are simply average values used by engineers to design machines. We also know that all of the state-of-the-gas variables will change with altitude, which is why the typical values are given at sea level, static conditions. Because the gravity of the earth holds theatmosphere to the surface, as altitude increases, air density, pressure, and temperature decrease.
The variation of the air from the standard can be very important since it affects flow parameters like the speed of sound. You will learn that jet engines do not produce as much thrust on hot, muggy days as on cold, crisp days, and that lift, drag, and thrust vary greatly with altitude. 17] Viscosity can be simply defined as the internal friction of a fluid caused by molecular attraction which makes it resist a tendency to flow. The viscosity of air is important when discussing airflow in the region very close to the surface of the aircraft. The viscosity of gases is unlike that of liquids, in that with gases an increase in temperature causes an increase in viscosity.
The coefficient of absolute viscosity has been assigned the symbol μ . Since aerodynamics often involves considerations f both viscosity and density, ma more usual form of viscosity measurement, known as kinematic viscosity, is often used. If you need to calculate the density of dry air, you can apply the ideal gas law. This law expresses density as a function of temperature and pressure.
Like all gas laws, it is an approximation where real gases are concerned but is very good at low pressures and temperatures. Increasing temperature and pressure adds error to the calculation. The addition of water vapor to air reduces the density of the air, which may at first appear counter-intuitive. This occurs because the molar mass of water (18 g/mol) is less than the molar mass of dry air (around 29 g/mol).
For any gas, at a given temperature and pressure, the number of molecules present is constant for a particular volume (see Avogadro's Law). So when water molecules are added to a given volume of air, the dry air molecules must decrease by the same number, to keep the pressure or temperature from increasing. Air - Specific Heat vs. Temperature at Constant Pressure - Online calculator with figures and tables showing specific heat of dry air vs. temperature and pressure. The calculator below can be used to calculate the air density and specific weight at given temperatures and atmospheric pressure. This is a good question to ask, because the air in a pipe friction loss, drag force, or pitot tube calculation, is indeed a real gas, not an ideal gas.
Fortunately, however, many real gases behave almost exactly like an ideal gas over a wide range of temperatures and pressures. The ideal gas law doesn't work well for very low temperatures or very high gas pressures . For many practical, real situations, however, the ideal gas law gives quite accurate values for the density of air at different pressures and temperatures. A property is a physical characteristic or attribute of a substance. Matter in either state, solid or fluid, may be characterized in terms of properties. For example, Young's modulus is a property of solids that relates stress to strain.
Density is a property of solids and fluids that provides a measure of mass contained in a unit volume. In this section, we examine some of the more commonly used fluid properties. Specifically, we will discuss 1) density, specific weight, and specific gravity, 2) bulk modulus, and 3) viscosity. Oxygen - Density and Specific Weight vs. Temperature and Pressure - Online calculator, figures and tables showing density and specific weight of oxygen, O2, at varying temperature and pressure - Imperial and SI Units. Helium - Density and Specific Weight vs. Temperature and Pressure - Online calculator, figures and tables showing density and specific weight of helium, He, at varying temperature and pressure - Imperial and SI Units. Ethane - Density and Specific Weight vs. Temperature and Pressure - Online calculator, figures and tables showing density and specific weight of ethane, C2H6, at varying temperature and pressure - Imperial and SI Units.
Argon - Density and Specific Weight - Online calculator, figures and tables showing density and specific weight of argon, Ar, at varying temperature and pressure - Imperial and SI Units. The density of air is the mass per unit volume of atmospheric gases. The density of air, or how light it is, depends on the temperature and pressure of the air.
Typically, the value given for the density of air is at STP . For any ideal gas, at a given temperature and pressure, the number of molecules is constant for a particular volume (see Avogadro's Law). If we can treat air as an ideal gas, then the ideal gas law in this form can be used to calculate the density of air at different pressures and temperatures. Coupled to the confusion that can arise from converting between different system of units are the "special" units used in the aircraft industries. These special units include the aptly named SLUG and the use of nautical terms for speed and distance . Operational (e.g. air traffic control and some flight instrument) parameters are often required when interpreting or confirming flight data.
(e.g., altitude is often quoted in feet (or thousands of feet, e.g. 33), rates of climb in feet per minute , weights in pounds , engine thrust in pounds, speed in nautical miles per hour and pressure in millibars. For liquids, mass density is not a strong function of temperature and pressure. Hence, density is generally assumed to be independent of the temperature and pressure for liquids. On the other hand, for gases, density varies with both temperature and pressure.
The relation between ρ, T and P for gases is given by the ideal gas law, which will be presented in a later section. It does not matter whether Equation 7-4 or Equation 7-5 is used to find sg because both relations yield the same value. The definitions given by Equation 7-4 and Equation 7-5 apply regardless of the temperature at which the specific gravity is being determined.
In other words, the reference temperature for water is always 4C, but the density and specific weight of the fluid being considered are based on the temperature specified in the problem. Table 7-1 summarizes the reference values used in the definitions of specific gravity. When working with a static gas, it is convenient to use specific volume, which is the volume divided by the mass. When a gas is moving, it is more convenient to use the density of a gas, which is the mass divided by the volume the gas occupies. Either variable can be used to define the state of the gas, since they are reciprocals.
The density , pressure, and temperature of a gas are related to each other through the equation of state. The state of a gas can be changed by external processes, and the reaction of the gas can be predicted using the laws of thermodynamics. A fundamental understanding of thermodynamics is very important in describing the operation of propulsion systems. TAS. True airspeed is CAS corrected for nonstandard pressure and temperature.
True airspeed and CAS are the same in standard atmosphere at sea level. But under nonstandard conditions, TAS is found by applying a correction for pressure altitude and temperature to the CAS. 15] The static pressure of the air P is simply the weight per unit area of the air above the level under consideration.
For instance, the weight of a column of air, with a cross sectional area of 1 ft2 and extending upward from sea level through the atmosphere is 2116 lb. The sea level static pressure is, therefore, 2116 psf (or 14.7 psi). Static pressure is reduced as altitude is increased because there is less air weight above.
At 18,000 ft altitude the static pressure is about half that at sea level. Where the constant of proportionality, , is called the dynamic viscosity. Equation 7-8 is known as Newton's law of viscosity, and fluids that conform to this law are referred to as Newtonian fluids. Common liquids such as water, oil, glycerin, and gasoline are Newtonian fluids as are common gases such as air, nitrogen, hydrogen and argon. The value of the dynamic viscosity depends on the fluid.
Liquids have higher viscosities than gases, and some liquids are more viscous than others. For example, oil, glycerin and other gooey liquids have higher viscosities than water, gasoline, and alcohol. The viscosities of gases do not vary significantly from one gas to another, however. The fluid properties density, specific weight, and specific gravity are measures of the heaviness of a fluid, but these properties do not completely characterize a fluid. Two different fluids, water and oil for example, have similar densities but exhibit distinctly different flow behavior. Water flows readily when poured from a container, whereas oil, which is a thicker fluid, flows more slowly.
Clearly, an additional fluid property is required to adequately describe the flow behavior of fluids. Viscosity may be qualitatively defined as the property of a fluid that signifies the ease with which the fluid flows under specified conditions. \(\) My derivation started with an ideal gas approximation of dry air and water vapor. The total pressure \(p\) is the summation of partial pressures for dry air \(p_d\) and water vapor \(p_w\). Since this would be a freezing temperature at sea level, dry air is less dense than the cited value most of the time. However, air typically contains a lot of water vapor, which would make it denser than the cited value.
Density altitude is a function of atmospheric pressure and temperature at a particular altitude . It is, in essence, the density of the standard atmosphere; however, the altitude value will either be greater or less than the true altitude depending on the condition of the air. Density is an attribute of substances defined as the ratio of mass to volume. The specific density of a gas is the ratio of the density of that gas to the density of air. On the other hand, specific weight is the ratio of the weight of a substance to its volume.
Dry Air and Water Vapor - Density and Specific Volume vs. Temperature - Imperial Units - Density and specific volume of dry air and water vapor at temperatures ranging 225 to 900 degF . EAS. Equivalent airspeed is CAS corrected for compression of the air inside the pitot tube. Equivalent airspeed is the same as CAS in standard atmosphere at sea level.
As the airspeed and pressure altitude increase, the CAS becomes higher than it should be and a correction for compression must be subtracted from the CAS. For example, the air is less dense in Denver than in Miami. The density of air decreases as you increase temperature, providing the volume of the gas is allowed to change. As an example, air would be expected to be less dense on a hot summer day versus a cold winter day, providing other factors remain the same. Another example of this would be a hot air balloon rising into a cooler atmosphere.
Density is affected not only by temperature and pressure but also by the amount of water vapor in the air. This occurs because the molecular mass of water is less than the molecular mass of air . For any gas, at a given temperature and pressure, the number of molecules present is constant for a particular volume. So when water molecules are introduced to the air, the number of air molecules must reduce by the same number in a given volume, without the pressure or temperature increasing.
Where ρ is the air density, p is pressure, R is the specific gas constant, and T is temperature in kelvins. Since the molecular mass weight of dry air is \( 28.97 \frac \) while water vapor is lower at \( 18.00 \frac \), the density of wet air is always lower than dry air. A cylindrical container with a height and diameter of 16 cm and 10 cm, respectively, contains 1.1 kg of liquid. If the liquid fills the container, find the density, specific weight, and specific gravity of the liquid.
Viscosity, like all physical properties, is a function of temperature. For liquids, dynamic viscosity decreases dramatically with increasing temperature. For gases, however, dynamic viscosity increases, but only slightly, with increasing temperature. The kinematic viscosity of liquids behaves essentially the same as dynamic viscosity because liquid densities change little with temperature. The kinematic viscosities of gases, however, increase drastically with increasing temperature because gas densities decrease sharply with increasing temperature. In the SI system of units, kinematic viscosity is expressed in m2/s, and in the English system it is expressed in ft2/s.
Because the ratio of dynamic viscosity to density often appears in the analysis of fluid systems, kinematic viscosity may be the preferred viscosity property. About density, specific weight,and specific gravity of fluids. Any gas has certain properties that we can detect with our senses. The values and relations of the properties define the state of the gas. The pressure of a gas equals theforce exerted by the gas divided by the surface area on which the force is exerted. The temperatureof a gas is a measure of how hot or cold the gas is.
Gas is composed of a large number of molecules, and the sum of the mass of all the molecules is equal to the mass of the gas. For a given pressure and temperature, the volume depends directly on the amount of gas. Since the mass and volume are directly related, we can express both the mass and volume by a single variable. Air - Specific Heat vs. Pressure at Constant Temperature - Figures and tables with isobaric and isochoric specific heat of air at constant temperature and pressure ranging 0.01 to bara. The symbol for absolute temperature is T, and the symbol for sea level standard temperature is T0. Using temperature ratios rather than actual temperatures cancels out the units and simplifies things.
In many college courses and industries, aeronautical calculations will be conducted in SI units (Systeme International d'Unites). This system has the basic units of kilogram, metre, second, Kelvin, and derived units of Newton, Joule, Pascal, Watt etc.. Unfortunately, not all aeronautical work is done in SI units. Some companies and some older reports will be in the old British System.
For example U.S. industries mainly use the old British System of foot, pound force, second and Rankin. Also, some European industries still use the Old Metric System metre, kilogram force, second and Kelvin. To work as an aeronautical engineer you will need to understand all these systems of measurement.
Unfortunately, it is common practice for a variety of different units to be used in most types of aircraft analysis. It is therefore necessary to understand, and be familiar with using and converting between any system of units. The value for the density of air at STP depends on the definition of STP. The definition of the temperature and pressure isn't standard, so the value depends on who you consult. Depending on the measuring instruments, use, area of expertise and necessary rigor of the result different calculation criteria and sets of equations for the calculation of the density of air are used. The altitude in the standard atmosphere corresponding to a particular value of air density.